By: Scott Simon
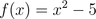
Since the opposite of x makes this function the same as it was with x, it is an even function.
Homework: section 1.2 #'s 47-49,51, 61-71 odd
Today in class we learned that functions can be even, odd, or neither even or odd.
A function is an even function when you plug in the opposite of x (which is negative x) for x and the function remains as it originally was.
Example:
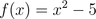
Since the opposite of x makes this function the same as it was with x, it is an even function.
If the opposite of x in a function makes it the opposite of the original function, then it is an odd function.
Example:
This looks like the opposite, but you have to check by solving for the opposite of the function, which means multiplying the whole function by -1. If it is not actually the opposite, then it is neither even nor odd.







No comments:
Post a Comment