Today we learned about right triangle trigonmetry and the six trigonometric functions. Consider a right traingle, one of whose acute angles is labeled theta. Relative to the angle theta, the three sides of the triangle are the hypotenuse, the opposite side, and the adjacent side.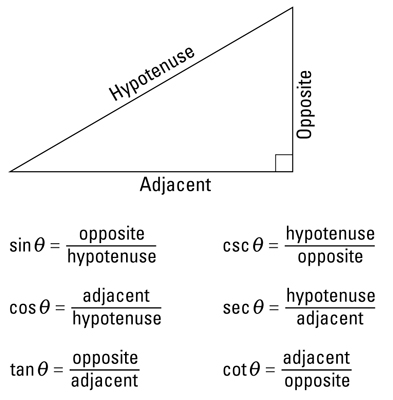

Note that the functions in the second row above are the reciprocals of the corresponding functions in the first row.
Find the exact values of the six trigonmetric functions of theta.

Find the exact values of the six trigonmetric functions of theta.
sin theta= 4/5
cos theta=3/5
tan theta=4/3
csc theta=5/4
sec theta= 5/3
cot theta=3/4
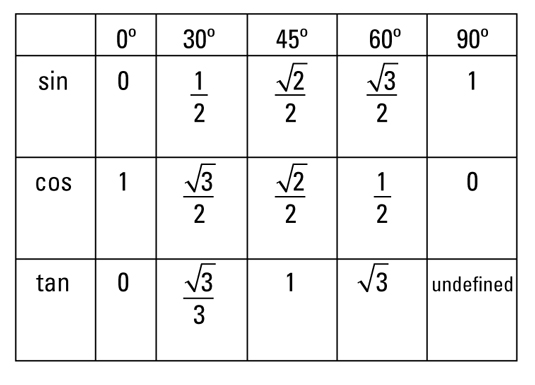 Note that sin 30 =1/2=cos 60. This occurs because 30 degrees and 60 degrees are complementary angles, and, in general, it can be shown from the right triangle definitions that confunctions of complementary angles are equal. That is, if theta, is an acute angle, the following relationships are true.
Note that sin 30 =1/2=cos 60. This occurs because 30 degrees and 60 degrees are complementary angles, and, in general, it can be shown from the right triangle definitions that confunctions of complementary angles are equal. That is, if theta, is an acute angle, the following relationships are true.sin(90 degrees-theta)= cos theta
tan(90 degrees-theta)=cot theta
sec(90 degrees-theta)=csc theta
cos(90 degrees-theta)=sin theta
cot(90 degrees-theta)=tan theta
csc(90 degrees-theta)=sec theta
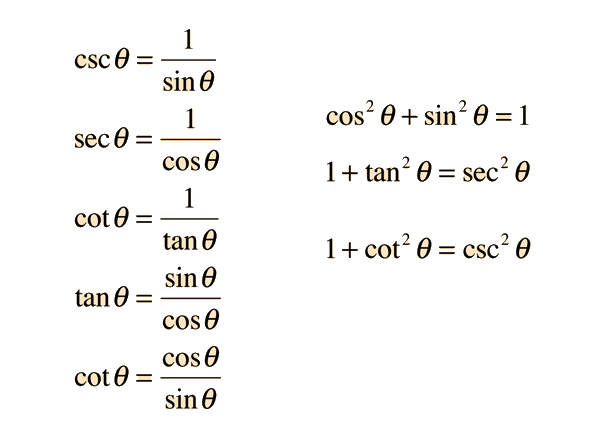
No comments:
Post a Comment