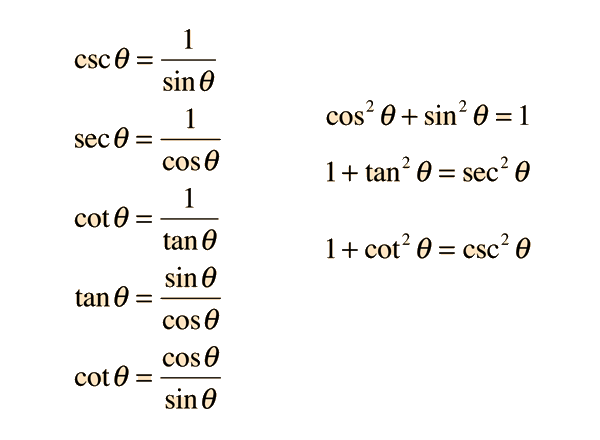4.3 Right Triangle Trigonometry

Today we learned about right triangle trigonmetry and the six trigonometric functions. Consider a right traingle, one of whose acute angles is labeled theta. Relative to the angle theta, the three sides of the triangle are the hypotenuse, the opposite side, and the adjacent side.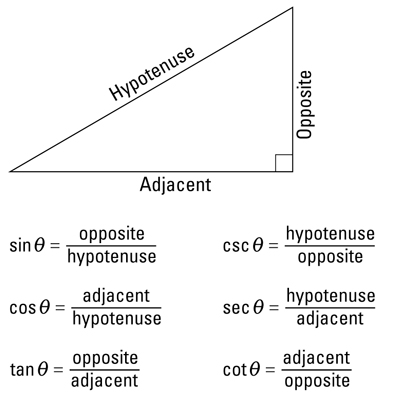

Note that the functions in the second row above are the reciprocals of the corresponding functions in the first row.
Find the exact values of the six trigonmetric functions of theta.

sin theta= 4/5

cos theta=3/5

tan theta=4/3

csc theta=5/4

sec theta= 5/3

cot theta=3/4

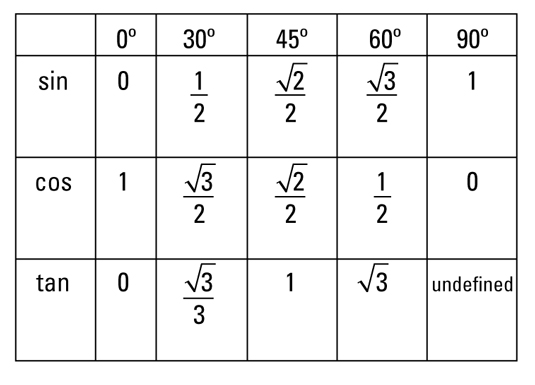Note that sin 30 =1/2=cos 60. This occurs because 30 degrees and 60 degrees are complementary angles, and, in general, it can be shown from the right triangle definitions that confunctions of complementary angles are equal. That is, if theta, is an acute angle, the following relationships are true.

sin(90 degrees-theta)= cos theta

tan(90 degrees-theta)=cot theta

sec(90 degrees-theta)=csc theta

cos(90 degrees-theta)=sin theta

cot(90 degrees-theta)=tan theta

csc(90 degrees-theta)=sec theta

4.1 Radian & Degree Measure

Trigonometry: Radian and Degree Measure

When the length of a segment of the circumference of a circle is equal to the radius, this is a measurement known as a radian. There are 2π radians in a circle.


There are 2π radians in one full revolution. 2π radians = 360º

To convert degrees to radians, you multiply the degree by π/180

For example, take 45º 45 • π/180 = 45π/180 = π/4

45º is the same measurement as π/4 radians


You can look at a circle as either 360º or 2π radians. Because it is all proportional, π radians is the same as 180º, π/2 radians is the same as 90º, π/4 is the same as 45º, etc.




Cosine is the x coordinate of the endpoint and sine is the Y coordinate.

When two measurements land on the same line, these measurements are called co-terminal. For example, π/4 radians is the same as 9π/4 radians, and because of this, they are co-terminal.

2.6 Rational Functions

Note: I could not upload pictures because of maintenance.

Today we learned about rational functions. This involved the format for a rational function which is,

f(x)=N(x)/D(x), where N(x) and D(x) are polynomials
 Ex: 2x^2+x-1/3x-1
 (Keep in mind D(x) cannot be to the degree of 0 otherwise it is just a normal polynomial)

Due to maintenance I could not insert graphs to show what this equation and other equations look like.

We also learned about the tendencies of these equations

ex. f(x)=2x/x-3

Here when x-> +/-infinity      f(x)->2
also when x->3       f(x)->+/-infinity

One of the major things we learned about in class were vertical and horizontal asymptotes which keep the points on the curve of the graph from going way too high, so that it would be almost impossible to measure.

Some rules of asymptotes that we learned were:
 The closer x gets to the vertical asymptote, the larger the y or f(x) value.

The larger x gets, the closer the y value is to the horizontal asymptote.

To find the vertical asymptotes, you take the denominator of the rational function and make it equal to zero. So to find the vertical asymptote of the equation above, we would do this:

x-3=0
x=3

Given this the vertical asymptote is 3.

To find the horizontal asymptote, there are three cases of how to find it.

Case One:  when a lower degree polynomial/higher degree polynomial, than the horizontal asymptote is 0.
ex. 2x/x^2-3
horizontal asymptote: y=0

Case Two: when to of the same degree polynomials are divided by each other, you take the coefficients of each of the first terms and divide those by each other. Once that is found, that is the horizontal asymptote.

ex. 2x/x-3
2/1=2 ----> horizontal asymptote: y=2

Case Three: when a higher degree polynomial/lower degree polynomial, there is no horizontal asymptote.

ex. 2x^2/x-3
No horizontal asymptote

2.4 complex numbers

In this chapter we solve complex equations by adding, subtracting, multiplying, and dividing.
we use the imaginary number i which is defined as the square root of -1.


If a and b are are real numbers, the number a + bi is a complex number. which is supposed to be written in standard form a+bi = c+di
iff a=c and b=d

If b is not = to zero, the number a+bi is an imaginary number

(4+4i) + (3-6i) = 7-2i addition of complex numbers

(4+4i) - (3-6i) = 1+10i subtraction of complex numbers

(4+4i)(3-6i) = 12 -12i -24i^2 i^2 =-1 -24(-1) =24 multiplication of complex numbers
= 36-12i

4+4i/3-6i multiply numerator and denominator by 3+6i to cancel out middle term
= -12+36i/9-36i^2

-12/45 + 36/45i
= -4/15+ 4/5 i (written in standard form) division of complex numbers


Expanding
zeros: 2, 3-4i, and 3+4i

f(x)= (x-2)(x-(3-4i))(x-(3+4i))
f(x)= (x-2)(x-3+4i)(x-3-4i)
(a + b) (a - b) = a^2 -b^2
f(x)= (x-2)(x-3)^2-(4i)^2

f(x)= x^3-8x^2+37x-50 (expanded)

Solutions to review

Answer key

Don't forget to check out Assignment 4 on your sheet for a nice overview of the kinds of problems you should be able to do.

2.3

In this lesson we talked about dividing polynomials. We used long division and synthetic division.

Long Division

x^3-3x^2-x+1+(1/x+3)
x+3/x^4+0x^3-10x^2-2x+4
-x^4+3x^3
-3x^3-9x^2
-x^2-2x
-x^2-3x
x+4
-x+3
1

Synthetic Division
This can only be used when the equation is linear and the leading term has a coefficient of one.

3/ 1 0 -10 -2 4
-3 9 3 -3

1 -3 -1 1 /1

1x^3-3x^2-x+1+(1/x+3)


We also talked about the Rational Rood Theorem

f(x)=px^n+...+q

factors of p/factors of q


Our homework was assignment 3
2.3 - 1-8, 11, 28-36 even, 39,45,48,63,96,102,103(a-f)

Chap. 2.2

Chapter 2.2 -Polynomial Functions of Higher Degree....check it out

-Assignment- 2.1 = 68(c-e), 73, 79, 80, & 85
2.2 = 1-8, 11, 22-36 even, 39, 45, 48, 63, 96, 102, 103(a-f)

-The Maximum number of intercepts for a Polynomial is the variables highest exponent.

extrema- relative minimums or maximums

Real Zeroes of Polynomial Functions-
1. x = a is a zero of the function
2. x = a is a solution of the polynomial equation f(x) = 0
3. (x-a) is a factor of the polynomial f(x)
4. (a,0) is an x-intercept of the graph of f

-Finding zeros of polynomial functions is closely related to factoring and finding x-intercepts

End Behavior
X -> 00 x -> -00
f(x) -> 00 f(x) -> 00

Example problem = 3x^5 - 7x^4 + 3x^3 - 2x + 1 = x -> 00 , f(x) -> 00

Intermediate Value Theorem - concerns the existence of real zeros of polynomial functions.
-theorem states that if (a, f(a)) and (b,f(b)) are two points on the graph of a polynomial functions such that f(a) can not = f(b), then for any number d between f(a) and f(b) there must be a number c between a and b such that f(c) = d


Helpful Video- http://www.youtube.com/watch?v=4TA5Zy8Hap8










-











-Leading Coefficient Test- Test used to determine whether the graph of a polynomial eventually rises or falls

Chapter 2 Section 1 - Quadratic Functions

• A polynomial function is of the form:
• f(x)=AnX^n+An-1X^n-1+An-2X^n-2+...+A2X^2+A1X+A0
• Quadratic Formula
• http://www.youtube.com/watch?v=H_7lNT9oDzI
• The value of n must be a nonnegative integer (i.e., it must be a whole number; it is equal to zero or a positive integer)
• The coefficients are An, An-1, ... A1, A0. <-- These are real numbers
• The degree of the polynomial function is the highest value of n
• f(x)=X^2+5X-7 (second degree)
• g(x)=2X^3-8+/X[square root of X]-1 (not a polynomial)
• h(x)=X^1/2+X-6 (not a polynomial)
• i(x)=4 (zero degree)
• k(x)=2^x (exponential function)
• Degree               |Name               |Example          

                     0             Constant            f(x)=4
                     1             Linear                g(x)=5x-3
                     2             Quadratic          h(x)=3x^2-9x+8
                     3             Cubic                i(x)=x^3
                     4             Quartic              j(x)=x^4
                     5             Quintic              k(x)=x^5

• Zeros, X-intercepts, f(x)=0, roots <-- All mean the same thing
• Standard form: f(x)=ax^2+bx+c
• Vertex form: f(x)=a(x-h)^2+k
• a: stands for the shrinking or stretching of the parabola
• h: determines whether it moves left or right
• k: symbolizes if it goes up or down
• Completing the square
• f(x)=x^2-6x+5
• f(x)=(x^2-6x+__)                                            +5
• take the +5 and put it far away from the equation, it'll be used later
• to find the square use the equation ((b/2)^2)
• f(x)=(x-3)^2 --> f(x)=(x^2-6x+9)+5
• seeing as f(x) isn't a number, because you add 9 to one side, you still have to subtract it
• that's were the last digit comes in
• f(x)=(x^2-6x+9)+(-9+5)
• f(x)=(x-3)^2-4
• vertex: (3,-4)

Homework: 2.1-#1-8, 12, 17, 20, 29, 31, 35, 37, 41, 54, 61, 65, 67, 69