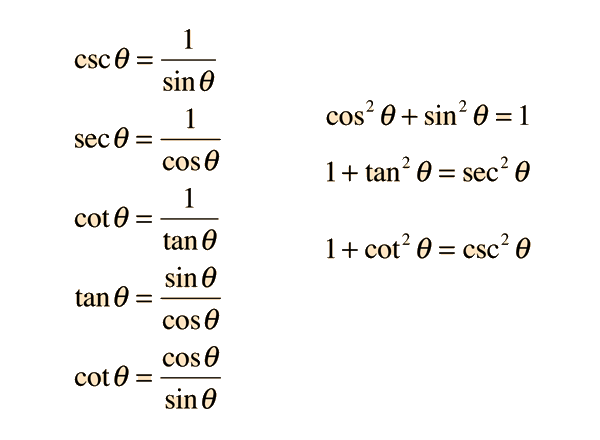Note: I could not upload pictures because of maintenance.
Today we learned about rational functions. This involved the format for a rational function which is,
f(x)=N(x)/D(x), where N(x) and D(x) are polynomials
Ex: 2x^2+x-1/3x-1
(Keep in mind D(x) cannot be to the degree of 0 otherwise it is just a normal polynomial)
Due to maintenance I could not insert graphs to show what this equation and other equations look like.
We also learned about the tendencies of these equations
ex. f(x)=2x/x-3
Here when x-> +/-infinity f(x)->2
also when x->3 f(x)->+/-infinity
One of the major things we learned about in class were vertical and horizontal asymptotes which keep the points on the curve of the graph from going way too high, so that it would be almost impossible to measure.
Some rules of asymptotes that we learned were:
The closer x gets to the vertical asymptote, the larger the y or f(x) value.
The larger x gets, the closer the y value is to the horizontal asymptote.
To find the vertical asymptotes, you take the denominator of the rational function and make it equal to zero. So to find the vertical asymptote of the equation above, we would do this:
x-3=0
x=3
Given this the vertical asymptote is 3.
To find the horizontal asymptote, there are three cases of how to find it.
Case One: when a lower degree polynomial/higher degree polynomial, than the horizontal asymptote is 0.
ex. 2x/x^2-3
horizontal asymptote: y=0
Case Two: when to of the same degree polynomials are divided by each other, you take the coefficients of each of the first terms and divide those by each other. Once that is found, that is the horizontal asymptote.
ex. 2x/x-3
2/1=2 ----> horizontal asymptote: y=2
Case Three: when a higher degree polynomial/lower degree polynomial, there is no horizontal asymptote.
ex. 2x^2/x-3
No horizontal asymptote









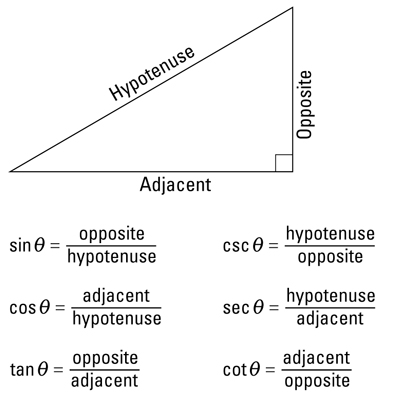

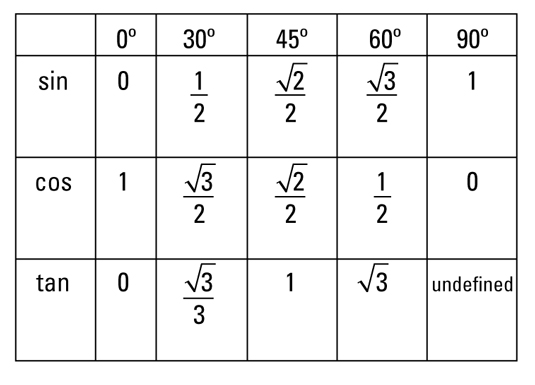 Note that sin 30 =1/2=cos 60. This occurs because 30 degrees and 60 degrees are complementary angles, and, in general, it can be shown from the right triangle definitions that confunctions of complementary angles are equal. That is, if theta, is an acute angle, the following relationships are true.
Note that sin 30 =1/2=cos 60. This occurs because 30 degrees and 60 degrees are complementary angles, and, in general, it can be shown from the right triangle definitions that confunctions of complementary angles are equal. That is, if theta, is an acute angle, the following relationships are true.